.jpg)

EEF: Improving Mathematics at Key Stage 2 and 3 -
Guidance Report Dena Jones, Evidence Lead in Education
The EEF brought out their first guidance report for maths back in 2017. As maths leader for my school, and more recently a Year 6 teacher, this report quickly became a litmus test to score our maths approach against. Ensuring we were aware of and applying the guidance was a continual and evolving task for all our teaching team. Over three instalments, I will aim to unpick the report, line it up against my understanding of cognitive theory and curriculum design and finally explain how we have adapted and refined our practice to take the most from it.
The report itself has eight main recommendations each split into various aspects within the elements.

|
|
Instinctively, I wanted to approach it as a box ticking exercise and RAG rate our practice against it. Indeed, they provide a broken-down version for this exact purpose. It soon became clear, however, that to do so was to skim over the interwoven fine nuance of the report and it was in here where the real use became clear. To use the over-quoted adage: it was worth more than the sum of its parts.
If we take strand 1 Assessment as our first example: firstly, I agree it should be number 1. But, if we arrange it like the first image below, it reminds us how assessment is the bedrock of everything else we do. It is continuous and influences what we do before, during and after any tasks, lessons and units of work.
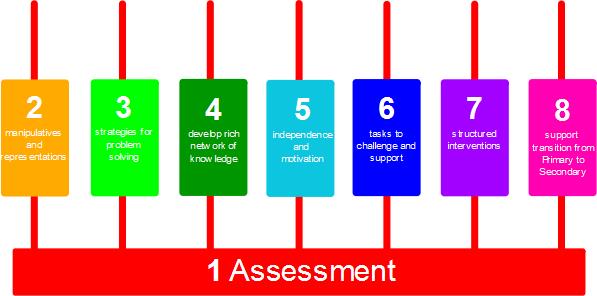
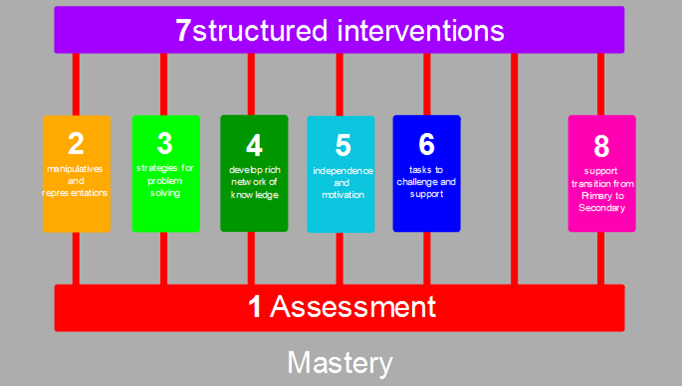
Alongside this underpinning assessment is our reaction to it. This is going to include recommendation 7 Interventions. In another blog, I am to delve into the details of ‘interventions’ but needless to say they ought to be in response to accurate and timely assessments.
Next, is a matter which isn’t in the report but is blatantly obvious when viewing the report as a whole - the undercurrent of mastery. If we lined up the guidance with what mastery seeks to exemplify, it would tick all the boxes.
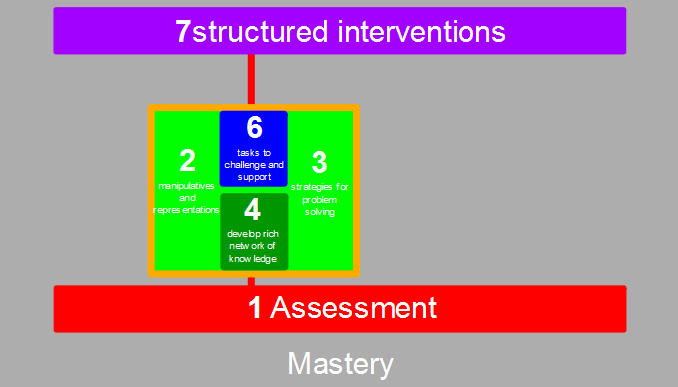
Returning to the report itself, what remains are elements which are linked significantly, and which provide such structural interplay that they cannot be evaluated in isolation of each other. Below we see this symbiotic relationship between strand 4 Developing rich network of knowledge and 6 Tasks to challenge and support. We toggle naturally between the two; one ineffective without the presence of the other. Furthermore, neither can establish a strong footing without the support of 2 Manipulatives and representations and 3 Strategies for problem solving. They almost become the ‘how’ alongside the ‘what’ that strands 4 and 6 provide.
Finally, while 8 Support transition from primary to secondary remains in place, I see an opportunity to move 5 Develop independence and motivation to the bedrock position beneath all other elements. The area of motivation is contentious, and one I will hopefully address in the next instalment, but it goes without saying that without a level of motivation and generating independence within children, our best laid plans for maths teaching and learning could be in jeopardy.
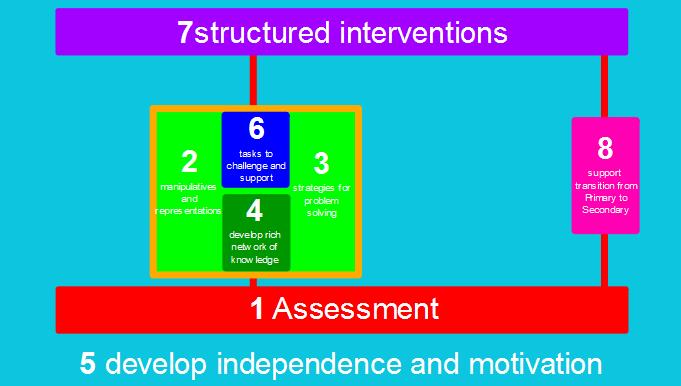
This reconsidered interpretation of the guidance fits more with how I believe maths is planned and delivered. Not in a linear scale that finishes one and moves on to the next. Of course, that was never what the EEF have intended for it to be, their report is obviously organised thoughtfully. But when it reaches the classroom, it becomes moulded in ways more akin to the above representations.
